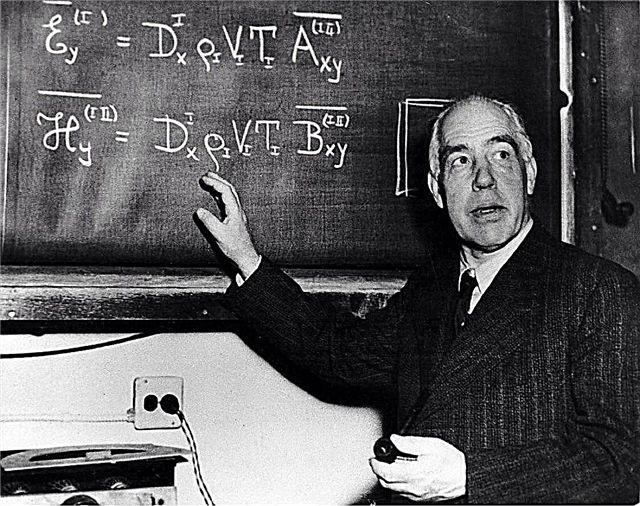Już starożytni greccy naukowcy zastanawiali się, czy człowiek stworzył matematykę, czy też ona istnieje i sama kieruje rozwojem Wszechświata, a człowiek jest w stanie tylko w pewnym stopniu pojąć matematykę. Platon i Arystoteles wierzyli, że ludzie nie mogą zmieniać matematyki ani wpływać na nią. Wraz z dalszym rozwojem nauki postulat, że matematyka jest nam dana z góry, paradoksalnie wzmocniony. Thomas Hobbes w XVIII wieku bezpośrednio napisał, że geometria jako nauka została poświęcona człowiekowi przez Boga. Laureat Nagrody Nobla Eugene Wigner już w XX wieku nazwał język matematyczny „darem”, jednak Bóg już nie był w modzie i według Wignera otrzymaliśmy dar od losu.

Eugene Wigner nazywano „cichym geniuszem”
Sprzeczność między rozwojem matematyki jako nauki a coraz większym umacnianiem wiary w z góry określoną z góry naturę naszego świata jest tylko pozorna. Jeśli większość pozostałych nauk dowiaduje się o świecie w zasadzie empirycznie - biolodzy znajdują nowy gatunek i opisują go, chemicy opisują lub tworzą substancje itp. - to matematyka dawno pozostawiła wiedzę eksperymentalną. Ponadto może utrudniać jego rozwój. Gdyby Galileo Galilei, Newton czy Kepler, zamiast postawić hipotezę o ruchu planet i satelitów, patrzyli w nocy przez teleskop, nie byliby w stanie dokonać żadnego odkrycia. Dopiero za pomocą obliczeń matematycznych obliczyli, gdzie skierować teleskop, i znaleźli potwierdzenie swoich hipotez i obliczeń. A skoro otrzymawszy harmonijną, matematycznie piękną teorię ruchu ciał niebieskich, jak można było przekonać się o istnieniu Boga, który tak skutecznie i logicznie ułożył Wszechświat?

Zatem im więcej naukowcy dowiadują się o świecie i opisują go metodami matematycznymi, tym bardziej zaskakująca jest zgodność aparatu matematycznego z prawami natury. Newton odkrył, że siła oddziaływania grawitacyjnego jest odwrotnie proporcjonalna do kwadratu odległości między ciałami. Pojęcie „kwadratu”, czyli drugiego stopnia, pojawiło się w matematyce dawno temu, ale w cudowny sposób znalazło się w opisie nowego prawa. Poniżej znajduje się przykład jeszcze bardziej zaskakującego zastosowania matematyki do opisu procesów biologicznych.
1. Najprawdopodobniej idea, że otaczający nas świat opiera się na matematyce, po raz pierwszy przyszła do głowy Archimedesowi. Nie chodzi nawet o słynne zdanie o punkcie podparcia i rewolucji świata. Archimedes oczywiście nie mógł udowodnić, że wszechświat opiera się na matematyce (i prawie nikt nie może). Matematykowi udało się poczuć, że wszystko w naturze można opisać metodami matematyki (oto punkt podparcia!), A nawet przyszłe odkrycia matematyczne są już gdzieś w przyrodzie zawarte. Chodzi tylko o to, aby znaleźć te wcielenia.

2. Angielski matematyk Godfrey Hardy tak bardzo chciał zostać naukowcem na fotelu, żyjącym w wysokim świecie abstrakcji matematycznych, że w swojej własnej książce, zatytułowanej żałośnie „Apologia matematyka”, napisał, że nie zrobił nic użytecznego w życiu. Szkodliwe, oczywiście, tylko czysta matematyka. Kiedy jednak niemiecki lekarz Wilhelm Weinberg badał właściwości genetyczne osobników kojarzonych w dużych populacjach bez migracji, udowodnił, że mechanizm genetyczny zwierząt się nie zmienia, posługując się jednym z dzieł Hardy'ego. Praca była poświęcona właściwościom liczb naturalnych, a prawo nazwano prawem Weinberga-Hardy'ego. Współautor Weinberga był ogólnie chodzącą ilustracją tezy „lepiej milczeć”. Przed przystąpieniem do prac nad dowodem tzw. Binarny problem Goldbacha czy problem Eulera (dowolną liczbę parzystą można przedstawić jako sumę dwóch liczb pierwszych) Hardy powiedział: każdy głupiec to zgadnie. Hardy zmarł w 1947 roku; nie znaleziono jeszcze dowodu na to.

Pomimo swoich ekscentryczności Godfrey Hardy był bardzo potężnym matematykiem.
3. Słynny Galileo Galilei w swoim traktacie literackim „Mistrz probierczy” bezpośrednio napisał, że Wszechświat, jak książka, jest otwarty dla każdego, ale tę książkę mogą czytać tylko ci, którzy znają język, w którym została napisana. I jest napisany w języku matematyki. W tym czasie Galileuszowi udało się odkryć księżyce Jowisza i obliczyć ich orbity oraz udowodnić, że plamy na Słońcu znajdują się bezpośrednio na powierzchni gwiazdy, używając jednej konstrukcji geometrycznej. Prześladowania Galileusza przez Kościół katolicki wynikały właśnie z jego przekonania, że lektura Księgi Wszechświata jest aktem poznania Boskiego umysłu. Kardynał Bellarmine, który rozważał przypadek naukowca w Najświętszej Kongregacji, od razu zrozumiał niebezpieczeństwo takich poglądów. To właśnie z powodu tego niebezpieczeństwa Galileo wyparł się uznania, że centrum wszechświata to Ziemia. Mówiąc bardziej nowocześnie, łatwiej było w kazaniach wyjaśnić, że Galileusz wkraczał w Pismo Święte, niż wykładać zasady podejścia do badania Wszechświata przez długi czas.

Galileo na procesie
4. Specjalista fizyki matematycznej Mitch Feigenbaum odkrył w 1975 roku, że jeśli mechanicznie powtórzysz obliczenia niektórych funkcji matematycznych na mikrokalkulatorze, wynik obliczeń zmierza do 4,669 ... Sam Feigenbaum nie potrafił wyjaśnić tej dziwności, ale napisał o tym artykuł. Po sześciu miesiącach recenzowania artykuł wrócił do niego, radząc mu, aby mniej zwracał uwagę na przypadkowe zbiegi okoliczności - w końcu matematyka. A później okazało się, że takie obliczenia doskonale opisują zachowanie ciekłego helu po podgrzaniu od dołu, przechodzenie wody w rurze w stan turbulentny (to wtedy woda wypływa z kranu z bąbelkami powietrza), a nawet kapanie wody przez luźno zakręcony kran.

Co mógł odkryć Mitchell Feigenbaum, gdyby w młodości miał iPhone'a?
5. Ojcem całej współczesnej matematyki, z wyjątkiem arytmetyki, jest Rene Descartes z układem współrzędnych nazwanym jego imieniem. Kartezjusz połączył algebrę z geometrią, przenosząc je na jakościowo nowy poziom. Uczynił matematykę prawdziwie wszechstronną nauką. Wielki Euklides zdefiniował punkt jako coś, co nie ma wartości i jest niepodzielne na części. U Kartezjusza punkt stał się funkcją. Teraz za pomocą funkcji opisujemy wszystkie nieliniowe procesy od zużycia benzyny po zmiany masy własnej - wystarczy znaleźć odpowiednią krzywą. Jednak zakres zainteresowań Kartezjusza był zbyt szeroki. Ponadto rozkwit jego działalności przypadł na czasy Galileusza, a Kartezjusz, zgodnie z własnym oświadczeniem, nie chciał opublikować ani jednego słowa, które byłoby sprzeczne z doktryną Kościoła. A bez tego, pomimo aprobaty kardynała Richelieu, został przeklęty zarówno przez katolików, jak i protestantów. Kartezjusz wycofał się do królestwa czystej filozofii, a potem nagle zmarł w Szwecji.

Rene Descartes
6. Czasami wydaje się, że londyński lekarz i antykwariusz William Stukeley, uważany za przyjaciela Izaaka Newtona, powinien zostać poddany niektórym procedurom z arsenału Świętej Inkwizycji. To jego lekką ręką legenda jabłka Newtona obiegła świat. Jakoś przychodzę do mojego przyjaciela Izaaka o piątej po południu, wychodzimy do ogrodu, a tam spadają jabłka. Weź Izaaka i zastanów się: dlaczego jabłka tylko spadają? Tak narodziło się prawo powszechnego ciążenia w obecności twego pokornego sługi. Całkowita profanacja badań naukowych. W rzeczywistości Newton w swoich „Matematycznych zasadach filozofii naturalnej” napisał bezpośrednio, że matematycznie wyprowadził siły grawitacji ze zjawisk niebieskich. Skala odkrycia Newtona jest obecnie bardzo trudna do wyobrażenia. W końcu wiemy już, że cała mądrość świata mieści się w telefonie i nadal będzie miejsce. Postawmy się jednak w sytuacji człowieka XVII wieku, który był w stanie opisać ruch prawie niewidzialnych ciał niebieskich i wzajemne oddziaływanie obiektów za pomocą dość prostych środków matematycznych. Wyraź wolę Bożą w liczbach. Ognie Inkwizycji już wtedy nie płonęły, ale przed humanizmem było co najmniej 100 lat. Być może sam Newton wolał, aby dla mas była to boska iluminacja w postaci jabłka i nie obalił tej historii - był osobą głęboko religijną.

Klasyczna fabuła to Newton i jabłko. Wiek naukowca jest wskazany poprawnie - w momencie odkrycia Newton miał 23 lata
7. Często można spotkać się z cytatem o Bogu autorstwa wybitnego matematyka Pierre-Simona Laplace'a. Kiedy Napoleon zapytał, dlaczego Bóg nie jest wspomniany ani razu w pięciu tomach Mechaniki Niebiańskiej, Laplace odpowiedział, że nie potrzebuje takiej hipotezy. Laplace był rzeczywiście niewierzącym, ale jego odpowiedzi nie należy interpretować w sposób ściśle ateistyczny. W polemice z innym matematykiem Josephem-Louisem Lagrange'em Laplace podkreślił, że hipoteza wyjaśnia wszystko, ale niczego nie przewiduje. Matematyk uczciwie zapewnił: opisał istniejący stan rzeczy, ale jak on się rozwinął i dokąd zmierza, nie mógł przewidzieć. I Laplace właśnie w tym widział zadanie nauki.

Pierre-Simon Laplace